Universität Paderborn - Home Universität Paderborn
Die Universität der Informationsgesellschaft

Compilation Methods SS 2013 - Assignment 7

Kastens, Pfahler, July 11, 2013

Exercise 1 (List Scheduling)

a)
Construct the data dependence graph (Slide 502) for the following sequence operations. Draw the nodes on the same level which have the same maximal distance to an end node. 
1:      t1 := a;
2:      t2 := b;
3:      t3 := c;
4:      t4 := t2 + t3;
5:      x := t4;
6:      t5 := t4 + t1;
7:      y := t5;
b)
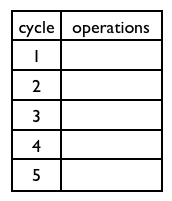
Apply list scheduling with the ASAP strategy (as soon as possible) (Slide 503, Slide 504) to construct the shortest possible schedule. Assume that each operation takes one cycle and that the target processor can execute at most 2 operations simultaneously.

c)
Apply list scheduling with the ALAP strategy (as late as possible) to construct the shortest possible schedule. Method: Invert the edges of the DDG and then apply ASAP. Assume that each operation takes one cycle and that the target processor can execute at most 2 operations simultaneously.

Exercise 2 (Loop Unrolling)

This is the body of the factorial loop (Slide C-5.6d) without the branch instructions: 

1: add #1, r1
2: mul r1, r5
3: add #4, r8
4: sto r5, m[r8]
a)
Construct and draw the data dependence graph (flow dependences only, no loop-carried dependences).
b)
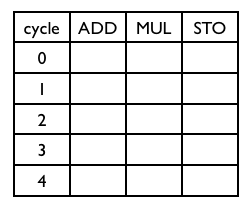
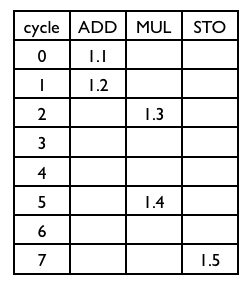
Construct a schedule for a LIW machine with 3 functional units: ADD, MUL, STORE. The result of an add operation is available in the next cycle, the mul operation needs two cycles, its result is written in the second cycle:
c)
Unroll the loop once. Construct and draw the data dependence graph with flow-, anti-, and output-dependences. Label the operations by 1.1 to 1.4, and 2.1 to 2.4. Do not represent dependences to or from operations of other iterations. Note: The add- and mul-operations are written in 2-address-form, i.e. the same register is used for the right operand and for the result.
d)
Construct a schedule for the unrolled loop body. Compare its length to the original schedule.

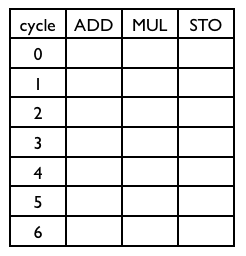
Exercise 3 (Software Pipelining)

Software pipelining is applied to a sequence of 5 instructions for a LIW machine with three functional units. A module schedule could be successfully constructed for an initiation interval of length 2:

Complete the following table such that it shows the prologue, the new loop body and the epilogue in the notation of Slide c-5.8.

Exercise 4 (Iteration spaces)

a)
Draw the shape of iteration spaces for the following loop nests in the style of Slide C-5.12a: 
1. for i = 0 to 5
      for j = -3 to 0

2. for i = 0 to 3
      for j = 2*i to 2*i+4

3. for i = 0 to 10
      for j = max (0, i-3) to min (i, 7)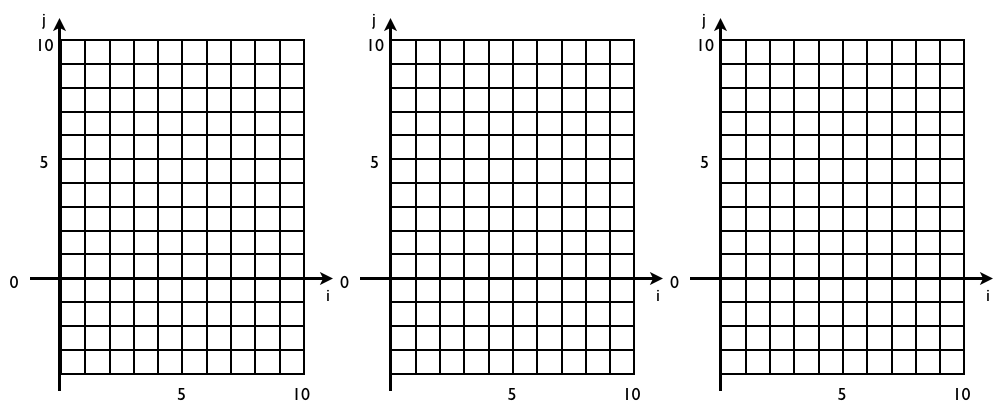

b)
Compute and draw dependence vectors (i, j) for the following assignments:
  1. a[i, j] = a[i, j-1] +a[i-2, j-1];
  2. a[i+3, j] = a[i-1, j+2];

Which of them are legal?

Give 2 examples for illegal dependence vectors.

Generiert mit Camelot | Probleme mit Camelot? | Geändert am: 13.06.2017