Grundlagen der Programmierung 2 SS 2005 - Lösung 1

Lösung zu Aufgabe 1

Zu dieser Aufgabe gibt es keine Musterlösung.

Lösung zu Aufgabe 2

Zu dieser Aufgabe gibt es keine Musterlösung.

Lösung zu Aufgabe 3

Hier finden Sie Die Lösung zu der ersten Aufgabe Notenspiegel.java. Wesentlich ist hier neben der Verwendung eines JFrame-Objekts das Einlesen aus einer Datei mit Hilfe der Stream-Klasse aus der Bibliothek javagently.jar im Directory /usr/java/upb-extension/.

Lösung zu Aufgabe 4

a)

In dieser Aufgabe ging es zunächst einmal darum, die Gamelet-Bibliothek anhand eines kleinen Beispiels und anhand der Dokumentation kennenzulernen.

Führt man das Beispielprogramm aus, ergibt sich z.B. folgendes Bild:

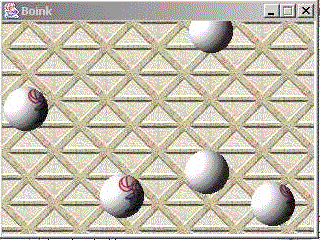
Die Kugeln werden an zufällig gewählte Stellen gesetzt und bewegen sich mit zufälliger Geschwindigkeit in irgendeine Richtung. Fliegt eine Kugel auf einer Seite aus dem Bild, erscheint sie nach einer gewissen Zeit auf der anderen Seite.

In Teil (a) war zusätzlich gefragt worden, wie ein Actor die Größe des sichtbaren Bereichs abfragen kann. Diese Frage konnte durch das Lesen des Beispielprogramms sowie der Dokumentation gelöst werden. Im Konstruktor der Klasse SimpleBall liest man:

  SimpleBall(Gamelet theGamelet) {
    ...
    setXPos(Gamelet.randBetween(0.0, theGamelet.getWidth() - getWidth()));
    setYPos(Gamelet.randBetween(0.0, theGamelet.getHeight()- getHeight()));

Der Dokumentation kann man entnehmen, daß die Klasse Gamelet die Methoden getWidth() und getHeight() zur Verfügung stellt. Weiterhin kann ein Actor nach seiner Konstruktion durch die Methode getGamelet() die Instanz der Klasse Gamelet abfragen. Bei der Konstruktion der SimpleBall-Objekte in Gamelet wird hierzu der Parameter this übergeben:

  public void createActors() {
    ...
    for (int i = 0; i < 5; i++) {
      addActor (new SimpleBall(this));
    }

b)

In Teil (b) sollte das Verhalten der Bälle so geändert werden, daß sie an den Rändern des Spielfeldes abprallen.

Eine Möglichkeit hierzu ist, nach jeder Aktualisierung der Position in calculateNewPosition() die aktuelle Position des Balls zu prüfen und ggf. die Position und die Geschwindigkeit des Balls zu ändern. Sinnvollerweise führt man hierzu eine Unterklasse von SimpleBall ein und erspart sich das fehleranfällige Abschreiben des Konstruktors aus SimpleBall. Die einzige verbleibende Änderung ist, daß nunmehr die Methode checkForOutOfBounds() nicht mehr ausgeführt werden muß, was durch Aufruf von setWrapAround(false) erreicht werden kann.

public class BounceBall extends SimpleBall {

  BounceBall(Gamelet theGamelet) {
    
    super(theGamelet);
    setWrapAround(false);
  }

Als nächstes muß die Methode calculateNewPosition() überschrieben werden. Innerhalb der Methode muß zunächst die Originalversion aufgerufen werden. Anschließend kann geprüft werden, ob der Ball außerhalb der Spielfläche liegt. Hierbei kann der Ball oben oder unten und links oder rechts aus dem Spielfeld gelangen. Dies schlägt sich in der Struktur der bedingten Anweisungen nieder.

  protected void calculateNewPosition() 
  {
    super.calculateNewPosition();
    
    <prüfe links und rechts>>
    
    <prüfe oben und unten>
  }

Zur Prüfung, ob sich der Ball links oder rechts außerhalb des Spielfeldes befindet, hilft die Betrachtung der folgenden Graphik. Eingezeichnet sind hier jeweils eine frühere Ballposition, die aktuelle Position in rot und die gewünschte neue Position in blau.

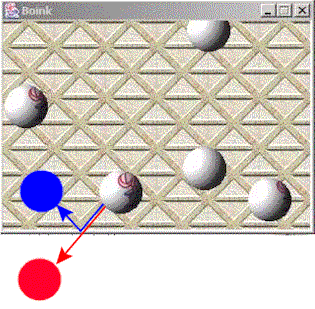
Ist ein Ball aus außerhalb des Spielfeldes, so muß seine Geschwindigkeit und Position korrigiert werden. Die Korrektur der Geschwindigkeit kann jeweils durch die Umkehrung des Vorzeichens der Geschwindigkeit erreicht werden. Zur Ermittlung der neuen Position betrachtet man die Ballkante, die den Spielfeldrand zuerst erreicht hat. Sie muß an der neuen Position genausoweit im Spielfeld sein, wie sie vorher außerhalb war. Falls W die Breite des Spielfeldes, w die Breite des Balles und x seine frühere Position ist, ergibt sich für die neue Position x' des Balles:

        x' + w = W - (x + w - W)
  <=>   x'     = W - x - w + W - w
  <=>   x'     = 2*(W - w) - x

Wie man dem Ergebnis ansieht, kann man einfacher die Reflektion von x an einem um die Breite der Kugel reduzierten Spielfeld betrachten. Setzt man die Abfragemethoden der Klasse Actor ein, ergibt sich für die Prüfung rechts und links folgendes Codefragment:

<prüfe rechts und links>:
    if (getXPos() < 0) {
      setXVelocity(- getXVelocity());
      setXPos(-getXPos());
    } else if (getXPos() >= (getGamelet().getWidth() - getWidth())) {
      setXVelocity(- getXVelocity());
      setXPos(2 * (getGamelet().getWidth() - getWidth()) - getXPos());
    }

Eine geringfügige Beschleunigung der Abarbeitung erhält man, wenn man die mehrfach benutzten Werte vorher an Variable zuweist. Dies ist hier aber nicht weiter ausgeführt. Ein entsprechendes Ergebnis erhält man für die Prüfung oben und unten.

Der vollständige Quelltext der Klasse BounceBall ist im Lösungsverzeichnis unter blatt1/boinkSolution erhältlich. In der Klasse Boink muß dann noch die Methode createActors() angepaßt werden.

Verständnisfrage: Kann der Ball trotzdem noch aus dem Spielfeld herausgeraten?

c)

In dieser Teilaufgabe sollte eine weitere Unterklasse von Actor implementiert werden. Die Hole genannte Klasse sollte ihre Objekte an einer zufälligen Stelle auf dem Spielfeld plazieren und sie nicht bewegen. Dies konnte durch Adaption des Konstruktors aus SimpleBall erreicht werden: Man setzt die Geschwindigkeit eines Lochs auf 0. Weiterhin muß ein anderes Bild geladen werden. Hierfür muß eine passende setImage-Methode aus Actor gewählt werden.

public class Hole extends Actor 
{
  Hole (Gamelet theGamelet) 
  {
    super(theGamelet);
    
    setImage(getGamelet().getImage("hole.gif"));
    setCurrentFrame(0);

    setXPos(Gamelet.randBetween(0.0, getGamelet().getWidth() - getWidth()));
    setYPos(Gamelet.randBetween(0.0, getGamelet().getHeight() - getHeight()));

    setXVelocity(0);
    setYVelocity(0);
    
    setWrapAround(false);
  }

  <Prüfung auf Zusammenstoß>
}

In der Aufgabe war gefordert, daß Bälle in Löcher fallen und verschwinden sollen. Der Dokumentation kann man entnehmen, daß die Methode collideWithActor(Actor other) aufgerufen wird, wenn festgestellt wird, daß sich die Bilder zweier Actor überlappen. Wird die Methode für ein Loch aufgerufen, kann es sich bei dem anderen Actor höchstens um einen Ball handeln. Löcher bewegen sich bekanntlich nicht und können deshalb auch nicht zusammenstoßen. (Falls sie nicht schon durch den Konstruktor übereinander gelegt wurden. Diese Möglichkeit wird hier ignoriert.)

Zur Implementierung des Verschwindens der Bälle wird deshalb die Methode collideWithActor(Actor other) überschrieben. Die neue Version prüft, ob der Radius des Loches größer als die Entfernung der Mittelpunkte von Ball und Loch ist. Hierzu wird die Summe der Quadrate der Entfernungen in X und Y-Richtung gebildet. Nach dem Satz von Pythagoras ist der Abstand die Wurzel dieser Summe. Ist der Ball dem Loch nah genug, wird mit Hilfe der Objektmethode removeActor aus der Klasse Gamelet der Ball entfernt.

<Prüfung auf Zusammenstoß>:

  protected void collideWithActor(Actor other) 
  {
    // Compute Distance of center points.

    double centerx = getXPos() + 0.5 * getWidth();
    double centery = getYPos() + 0.5 * getHeight();
    
    double otherx = other.getXPos() + 0.5 * other.getWidth();
    double othery = other.getYPos() + 0.5 * other.getHeight();
    
    double distance = 
      Math.sqrt((otherx - centerx) * (otherx - centerx) + 
		(othery - centery) * (othery - centery));
    
    double radius = 0.5 * getWidth();
    
    if (distance < radius) {
      getGamelet().removeActor(other);
    }
  }

Der vollständige Quelltext der Klasse Hole ist im Lösungsverzeichnis unter blatt1/boinkSolution erhältlich. In der Klasse Boink muß dann noch die Methode createActors() angepaßt werden. Bei der Ausführung ergibt sich dann z.B. folgendes Bild: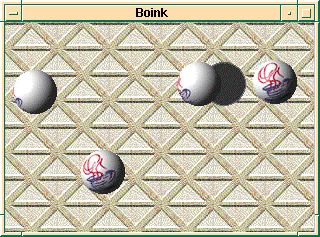

Generiert mit Camelot | Probleme mit Camelot? | Geändert am: 03.06.2005

Weiter zum Anfang