Funktionale Programmierung SS 2013 - Aufgabenblatt 2

Prof. Dr. U. Kastens
Institut für Informatik, Fakultät für Elektrotechnik, Informatik und Mathematik, Universität Paderborn
29.04.2013

Die Aufgaben auf diesem Blatt sollen in der Programmiersprache SML gelöst werden. Wir empfehlen folgende Arbeitsweise: Schreiben Sie Ihre SML-Funktionen in eine Datei, z.B. lsg.sml. Zum Starten des SML-Interpreters öffnen Sie ein Terminal und rufen das Kommando sml lsg.sml auf. Der SML-Interpretierer liest Ihre Definitionen ein und prüft sie. Im Erfolgsfall zeigt der Interpreteter die Werte oder Signaturen, die er ermittelt hat. Interaktiv haben Sie dann die Möglichkeit Ihre Funktionen aufrufen und auswerten zu lassen.

Hinweis: Eventuelle Warnungen von SML, dass Sie "polyequal" verwenden, unterdrücken Sie, wenn Sie den Interpretierer wie folgt aufrufen:

   sml -Ccontrol.poly-eq-warn=false

Aufgabe 1 (Erste Schritte mit SML)

a): Schreiben Sie eine Funktion wuerfelA(x), die die Oberfläche eines Würfels mit Kantenlänge x berechnet. Verwenden Sie die val wuerfelA = ... Notation.
b): Schreiben Sie eine Funktion wuerfelB(x), die das Volumen eines Würfels mit Kantenlänge x berechnet. Verwenden Sie die fun wuerfelB ... Notation.
c): Schreiben Sie eine Funktion ggt(a,b), die den größten gemeinsamen Teiler von a und b berechnet.
d): Schreiben Sie eine Funktion reverse(l), die die Umkehrung einer Liste erzeugt. Entwickeln Sie 2 Versionen der Funktion: mit und ohne Pattern Matching. Folie 401 zeigt gängige Operationen auf Listen.

(Hier ist die Lösung zu Aufgabe 1)

Aufgabe 2 (Closures)

a): Schreiben Sie eine Funktion wtab(f,s,t), die als Ergebnis eine Wertetabelle als Liste (f(s),f(s+1),...,f(t-1),f(t)) liefert. Verwenden Sie die Funktion um die Zweierpotenzen von 2⁰ bis 2¹⁰ zu erzeugen.
b): Schreiben Sie eine Funktion gerade(m,b,s,t), die eine Wertetabelle für eine Gerade mit der Steigung m und dem Y-Achsen-Schnittpunkt b liefert. Verwenden Sie dabei die Funktion wtab. Welche Bindungen sind in der Closure von wtab enthalten?

(Hier ist die Lösung zu Aufgabe 2)

Aufgabe 3 (Typ-Inferenz)

a)

Schreiben Sie eine Funktion g mit folgender Signatur:

   ('a->'b) * ('b->'c) ->  ('a->'c)

Verwenden Sie den SML-Interpretierer zur Überprüfung.

b)

Bestimmen Sie die Signaturen:

   fun x(li,m) = if null li
                 then 0
                 else x(tl li,m) + (if hd li = m then 1 else 0);

   fun y(f,nil) = nil
   | y(f,x::xs) = f x :: y(f,xs);

   fun z(a,b,c) = if null c
                  then nil
                  else if b
                       then a
                       else 1.5 :: tl c;

c)

Hausaufgabe: Geben Sie das Gleichungssystem für die Typinferenz der folgenden Funktion gemäß Folie 311 an. Welche Signatur hat die Funktion?

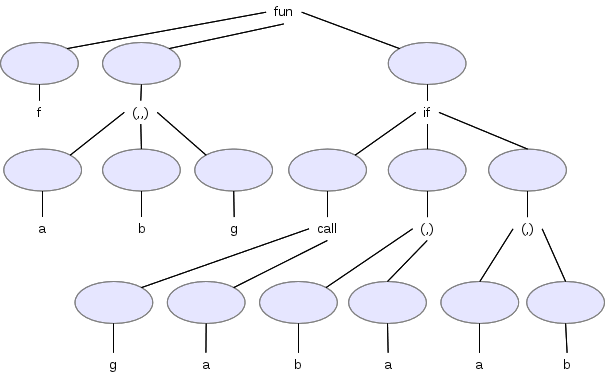
   fun f (a,b,g) = if g(a) then (b,a) else (a,b)

(Hier ist die Lösung zu Aufgabe 3)

Aufgabe 4 (Mengen-Implementierung, Akkumulierende Parameter)

Wir implementieren Mengen durch SML-Listen. Dabei ist natürlich wichtig, dass Elemente nur einmal in einer Liste vorkommen dürfen.

a)

Implementieren Sie die Funktionen

   fun member(el, set)
   fun insert(el, set)
   fun delete(el, set)

b)

Untersuchen Sie, welche der drei Funktionen zentral-rekursiv sind geben Sie endrekursive Versionen mit akkumulierendem Parameter an.

c)

Implementieren Sie die Funktionen

   fun unite(set1, set2) (* Vereinigung *)
   fun dissect(set1, set2) (* Schnitt *)

(Hier ist die Lösung zu Aufgabe 4)

Generiert mit Camelot | Probleme mit Camelot? | Geändert am: 13.05.2013

Weiter zum Anfang