Funktionale Programmierung SS 2013 - Aufgabenblatt 4

Prof. Dr. U. Kastens
Institut für Informatik, Fakultät für Elektrotechnik, Informatik und Mathematik, Universität Paderborn
27.05.2013

Aufgabe 1 (Wechselseitige Rekursion)

Wechselseitig rekursive Funktionen werden in einer Gruppe von Definitionen mit and verknüpft definiert, siehe auch Folie 306. Hier ist ein Beispiel:

   fun outside("("::"*"::t) = inside(t)
   |   outside(h::t) = h::outside(t)
   |   outside nil = nil and
       inside ("*"::")"::t) = outside(t)
   |   inside (h::t) = inside(t)
   |   inside nil = nil;
   
   outside ["c","l","a","s","s"," ","(","*","k","e","y","*",")"," ",
            "n","a","m","e"," ","(","*","i","d","*",")"," ","b","o","d","y",";"];

a): Was leisten diese beiden Funktionen?
b): Eliminieren Sie die wechselseitige Rekursion.

(Hier ist die Lösung zu Aufgabe 1)

Aufgabe 2 (Datentyp Baum)

Folie 504 zeigt die Definition des Datentyps Binärbaum:

   datatype 'a tree = Lf |
                      Br of 'a * 'a tree * 'a tree;

a): Verallgemeinern Sie diese Definition zu einem Typ für allgemeine Bäume (beliebig viele Kinder).
b): Geben Sie eine verallgemeinerte Version der Funktion size von Folie 504 an. Erproben Sie die Funktion an folgendem Baum: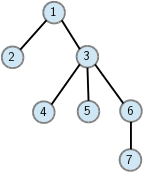

(Hier ist die Lösung zu Aufgabe 2)

Aufgabe 3 (Typdefinition und Ausnahme-Auslösung)

Gegeben ist die folgende unvollständige abstrakte Datentyp-Definition für einen Keller:

   abstype 'a stack = SEmpty | SCons of 'a * 'a stack
   with
     exception ExEmpty;
     val empty           = (*...*);
     fun push (s,v)      = (*...*);
     fun pop(SCons(v,s)) = (*...*);
     fun top(SCons(v,s)) = (*...*);
   end;

Die Funktion push liefert den Stack, der sich ergibt, wenn man in s den Wert v einfügt.
Die Funktion pop liefert den Stack, der sich ergibt, wenn man aus s das oberste Element entfernt.
Die Funktion top liefert das oberste Element des Stacks.

a)

Ergänzen Sie die Funktionen push, pop und top (Folie 505). Sehen Sie die Auslösung der angegebenen Ausnahme vor, falls der Keller unzulässig verwendet wird.

b)

Erproben Sie Ihren Keller-Typ, indem Sie einen Auswerter für Postfix-Ausdrücke entwickeln. Dazu sind folgende SML-Definitionen gegeben:

   datatype operation = plus | times;
   datatype elem = oper of operation | value of int;
   
   (* Beispiel: Der Postfix-Ausdruck "2 16 * 10 +" *)
   val e42 = [value(2), value(16),  oper(times), value(10), oper(plus)];
   
   fun stackeval  (* Ergänzen *)
   
   fun evaluate(expr) = stackeval(expr, empty);
   evaluate(e42);

(Hier ist die Lösung zu Aufgabe 3)

Aufgabe 4 (Ausnahme-Behandlung)

a)

Schreiben Sie eine Funktion eval, die den Dezimalwert von Binärzahlen berechnet. Die Binärzahlen sind als Folge von Ziffern gegeben.

   eval [1,0,1,0,1,0]; (* liefert 42 *)

b)

Ergänzen Sie eine Fehlerbehandlung, falls andere Ziffern als 0 und 1 vorkommen. In dem Fall soll eine Ausnahme ausgelöst werden. Diese Ausnahme soll im Aufruf-Kontext vom eval so behandelt werden, dass der Wert des betroffenen Ausdrucks -1 ist (Notation in SML: ~1).

(Hier ist die Lösung zu Aufgabe 4)

Generiert mit Camelot | Probleme mit Camelot? | Geändert am: 10.06.2013

Weiter zum Anfang