Funktionale Programmierung SS 2013 - Lösung 7

Prof. Dr. U. Kastens
Institut für Informatik, Fakultät für Elektrotechnik, Informatik und Mathematik, Universität Paderborn
08.07.2013

Lösung zu Aufgabe 1

a)

Die Funktion next definiert den Suchraum dergestalt, dass jeder Knoten als Inschrift einen String über {0,1}_* und zwei Unterbäume mit der gleichen Inschrift mit vorrangestellter "0" bzw. "1" hat.

b)

Definition der Funktion pred so, dass alle Strings, die den Teil-String 101010 beinhalten, zur Lösung gehören:

   fun pred n = String.isSubstring "101010" n;

   take (breadthFirst (next, pred) "", 16);

  (* liefert:
  ["101010","1010100","0101010","1101010","1010101","10101000","01010100",
   "11010100","00101010","10101010","01101010","11101010","10101001",
   "01010101","11010101","10101011"]
  *)

Lösung zu Aufgabe 2

a)

Kommentierung der Funktions-Definitionen:

   (* Fakultätsfunktion definiert mit Pattern-Matching *)
   factorial1 0 = 1
   factorial1 n = n * factorial1 (n - 1)

   (* Fakultätsfunktion definiert mit bedingtem Ausdruck *)
   factorial2 n = if n > 0 then n * factorial2 (n-1) else 1
    
   (* Fakultätsfunktion definiert durch Anwendung der Produkt-Funktion auf die Liste
      der Zahlen von 1 bis n *)
   factorial3 n = product [1..n]

b)

Eine Definition der Fakultätsfunktion, die die Funktion foldl verwendet:

mul a b = a*b
factorial4 n = foldl mul 1 [1..n]


-- oder
-- factorial4 n = foldl (\x y -> x*y) 1 [1..n]

-- oder einfach: 
-- factorial4 n = foldl (*) 1 [1..n]

c)

Die Fakultätsfunktionen können nun im interaktiven Haskell-Interpreter ghci verwendet werden.

Lösung zu Aufgabe 3

a)

Die Liste odds der ungeraden natürlichen Zahlen:

   genodds n = n : genodds (n+2)
   odds = genodds 1
   take 10 odds
   -- liefert [1,3,5,7,9,11,13,15,17,19]

b)

Alternative Definition von odds mit Hilfe des vordefinierten Funktionals iterate:

   odds = iterate (+2) 1

Hinweis: Haskell unterstützt aritmethische Folgen auch durch eine spezielle Syntax:

   odds = [1,3..]

c)

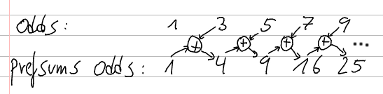
Die Funktion prefsums mit akkumulierendem Parameter:

   prefsums list = let aprefsums (h:t) s = (s+h) : aprefsums t (s+h)
                   in aprefsums list 0

Die Funktion prefsums mit verschränkten Strömen:

prefsums list = (head list) : [a+b | (a,b) <- zip (prefsums list) (tail list)]

Lösung zu Aufgabe 4

Näherungsverfahren für den Kehrwert 1/a einer Zahl a > 0:

   within eps (h1 : (h2: t)) = if abs(h1-h2) < eps
                               then h2
                               else within eps (h2:t)

   nextapprox a x = 2 * x - a * x * x

   kehrwert a = within 1e-9 (iterate (nextapprox a) 0.001)

   -- startwert x0, hier 0.001 muss zwischen 0 und 1/a liegen.
   -- obige kehrwert-funktion funktioniert also bis a = 1000

Generiert mit Camelot | Probleme mit Camelot? | Geändert am: 10.07.2013

Weiter zum Anfang