Parallel Programming WS 2014/2015 - Assignment 5

Kastens, Pfahler
Institut für Informatik, Fakultät für Elektrotechnik, Informatik und Mathematik, Universität Paderborn

Jan 05, 2015

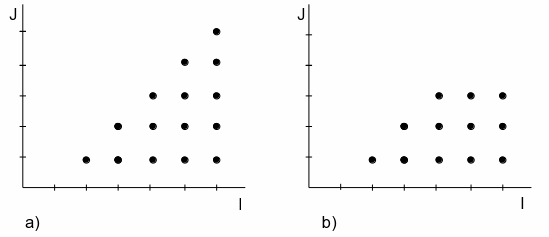
Exercise 1 (Iteration Spaces)

Determine the loops which have the following iteration spaces:

Exercise 2 ( Loop Permutation)

   for I = 1 to 6 do
     for J = 1 to 5 do
       A[I, J] = A[I - 1, J - 2] + 1
     endfor                    
   endfor

a)

Determine the dependence vector.

b)

Can we permute the I and J loops?

c)

Show that we cannot permute the I and J loops of the following loop nest:

   for I = 1 to N do
     for J = 1 to N do
       B[I, J] = B[I - 1, J + 1] + 1
     endfor                    
   endfor

(Here is the Solution for Exercise 2)

Exercise 3 ( Loop Reversal)

a)

Can we reverse the following loop?

   for I = 1 to 6 do
       B[I] = B[I - 1] + 1
   endfor

b)

Can we reverse the J loop?

   for I = 1 to 5 do
     for J = 1 to 6 do
       A[I, J] = A[I - 1, J - 1] + 1
     endfor                    
   endfor

(Here is the Solution for Exercise 3)

Exercise 4 ( Loop Skewing)

Original loop:

   for I = 1 to 3 do
     for J = 1 to 3 do
       A[I, J] = A[I - 1, J + 1] + 1
     endfor                    
   endfor

a): Draw the iteration space including a dependence vector.
b): Why is it illegal to permute the I and J loops?
c): Apply a skewing transformation with factor 1.
d): Draw the resulting iteration space including a dependence vector.
e): Permute the I and J loops of the resulting code. Is this a legal transformation?
f): Draw the resulting iteration space including a dependence vector.
g): Derive the loop bounds of the transformed loop from the drawing.
h): Homework: Derive the loop bounds mathematically using the transformation matrix.

(Here is the Solution for Exercise 4)

Exercise 5 (Homework: Transformation and Parallelization of a Loop)

Apply the transformation steps outlined on Slide 56c to parallelize the loop

   for I = 0 to N do
     for J = 0 to M do
       A[I + 1, J] = A[I, J - 1] + A[I + 1, J - 2]
     endfor                    
   endfor

These are the necessary steps:

1. Draw the iteration space.
2. Compute the dependence vectors and draw examples of them into the iteration space.
3. Apply a skewing transformation with factor 1 and draw the iteration space.
4. Apply a permutation transformation and draw the iteration space.
5. Compute the matrix of the composed transformation and use it to transform the dependence vectors.
6. Compute the inverse of the transformation matrix and use it to transform the index expressions.
7. Specify the loop bounds by inequalities and transform them by the inverse of the transformation matrix.
8. Write the complete loops with new loop variables ip and jp and new loop bounds.

Check your transformation. Assume N = M = 2. The original loop nest computes:

   s00: A[1, 0] = A[0, -1] + A[1, -2]
   s01: A[1, 1] = A[0, 0] + A[1, -1]
   s02: A[1, 2] = A[0, 1] + A[1, 0]
   
   s10: A[2, 0] = A[1, -1] + A[2, -2]
   s11: A[2, 1] = A[1, 0] + A[2, -1]
   s12: A[2, 2] = A[1, 1] + A[2, 0]
   
   s20: A[3, 0] = A[2, -1] + A[3, -2]
   s21: A[3, 1] = A[2, 0] + A[3, -1]
   s22: A[3, 2] = A[2, 1] + A[3, 0]

Compare this to your transformed version. Verify that the inner loop can be executed in parallel.

(Here is the Solution for Exercise 5)

Generiert mit Camelot | Probleme mit Camelot? | Geändert am: 19.01.2015

Weiter zum Anfang